这一篇,主要通过数学推导向量代数的方法,来编码求解线段交点,这也是最流行的方法,代码实现非常简单,另外,通过向量计算的方式得到交点,好处有三点:
1:支持三维空间的向量交点计算,这是通过方程组无法解决的问题,因为两个三元一次方程组,会得到无穷多的解,这些解实为两个平面交线上的所有点。
2:可以通过辅助参数 t 、u 是否在 [0, 1] 内,自行判断交点是否在线段上。
3:最终的结果完全由 4 个端点坐标得来,无需计算直线方程
推导过程比较长,如果想直接看代码,可以直接跳到结尾;虽然最终的代码实现很简单,但数学原理并不简单。最终的数学结论先写在下边,如果不想看证明,也可以直接套用下边的公式,求交点坐标:
四个端点坐标以及 Δ 值:a(x1, y1), b(x2, y2), c(x3, y3), d(x4, y4) deltaX1 = x2 - x1 deltaY1 = y2 - y1 deltaX2 = x4 - x3 deltaY2 = y4 - y3 行列式,det = 0,线段重叠或者平行: det = deltaX1 * deltaY2 - deltaX2 * deltaY1 辅助参数 t, u: t = (deltaX2 * (y1 - y3) - deltaY2 * (x1 - x3)) / det u = (deltaX1 * (y1 - y3) - deltaY1 * (x1 - x3)) / det 当 t、u 在 [0, 1] 内,表示有交点,交点坐标: x = x1 + t * deltaX1 y = y1 + t * deltaY1
下面开始数学推导。
一:向量和点的关系
先来简单的说明一下向量和点的关系,这也是该方法的核心:
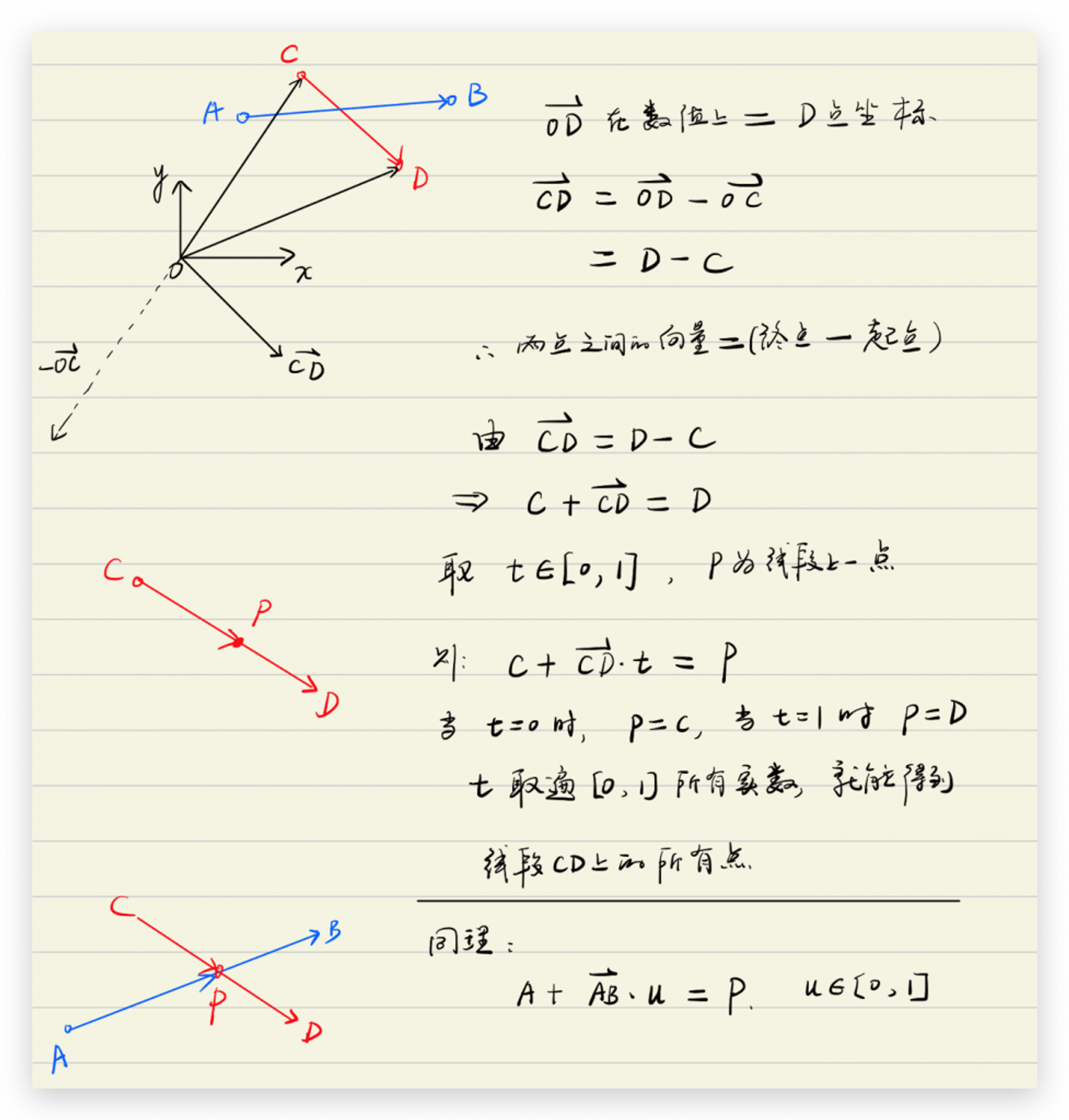
上图主要说明了三点数学问题:
1:向量和点在数值上是一样的
2:证明向量=(终点-起点)
3:由于 P 点作为线段公共交点,所以通过两条线段均可得到向量OP的值,即P点坐标(数值上一样),依次建立方程,求解辅助参数 t 和 u。
详细的推导过程
有了上边的基础,我们就可以列出两个等式,然后通过系数矩阵进行推导:


代码实现
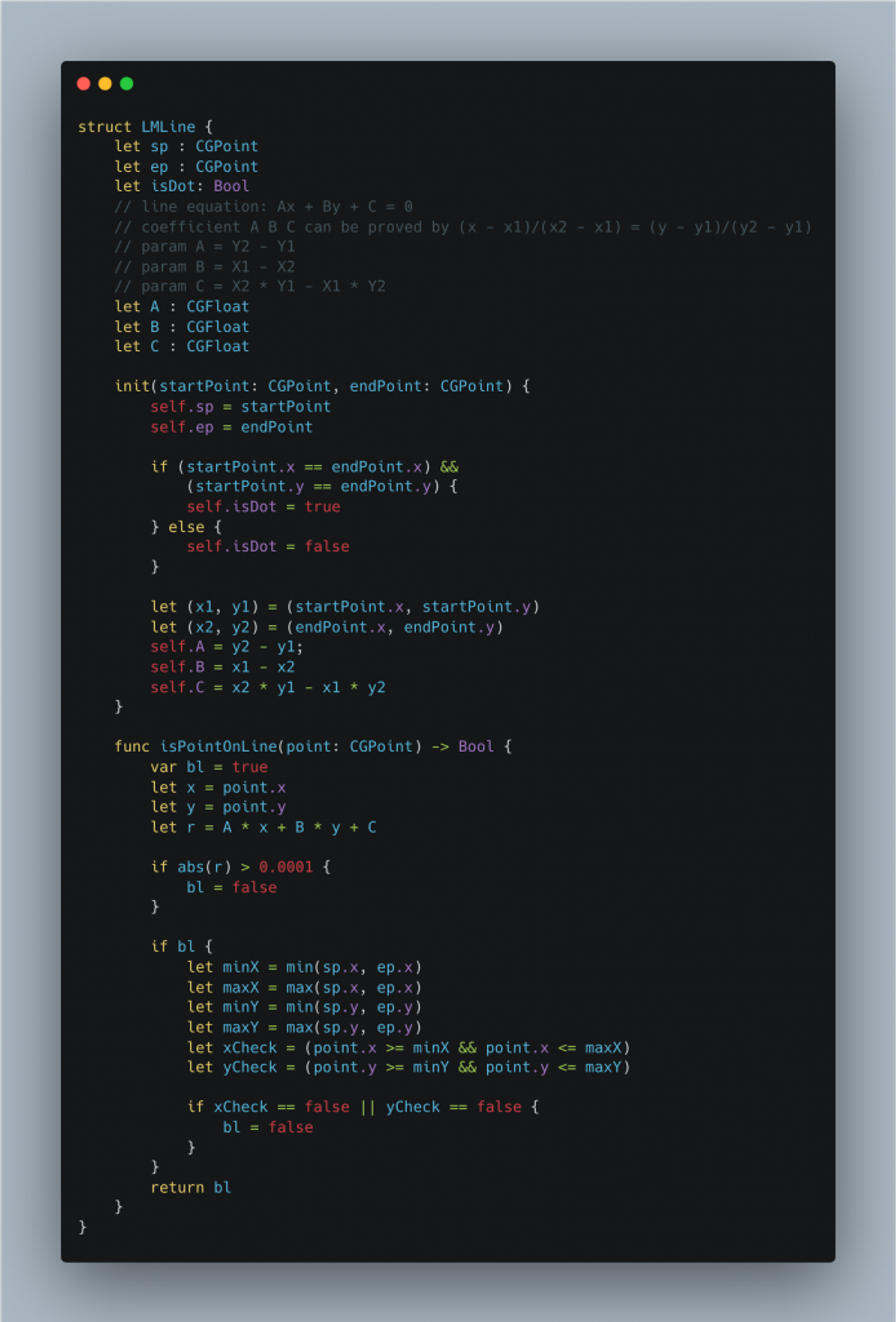
由于该方法,可以自行判断点是否在线段上,所以 Line 结构体的定义也很简单了: