乐理基础
断断续续的自学吉他有 4-5 年了,对乐理的一些基本概念一直比较模糊,最近花了点时间学习了下,梳理了一下,简单记录一些。
唱名
我们跟着简谱学唱的时候,看着 1155665,唱的却是 Do Do Sol Sol La La Sol,Do … 被称为唱名。
ㅤ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8(表示高一个8度的 1) |
唱名 | Do | Re | Mi | Fa | Sol | La | Ti | Do[8] |
Do[8] 表示的是比 Do[1] 高了一个八度的 Do;乐谱中高一个 8 度的 1,会在 1 头上点个黑点 · ,这里为了方便直接用 8 ,‘[]’ 也是用来表示音高的辅助工具,下同。
八度是什么
声音是靠振动产生的,Do[8] 比 Do[1] 高,这里的高指的是发声时的振动频率的高低,称为音高。声音的大小叫音量。乐理中把 Do[1] 到 Do[1] 称为一度,Do[1] 到 Re[2] 称为二度,因此从 Do[1] 到 Do[8] 之间的音程距离被称为八度。所以 ‘几度’ 其实是音程单位。
八度是可以继续向上叠加的,比如 Do[15] Re[16],就是振动频率更高的 Do[1] Re[2];具体从振动频率(单位 Hz)来看,八度就是二倍振动频率关系,假设 Do[1] 的振动频率是 230Hz,那么 Do[8] 的振动频率就是 460Hz,Do[1]的二倍,同样 Re[2] Mi[3] … Ti[7] 与相邻的高八度 Re[9] Mi[10] … Ti[14] 之间振动频率依然是二倍关系。
人耳的听觉就是这么神奇,能够比较轻松的分辨二倍振动频率关系的音高;需要注意的是,Do[15] 是 Do[1] 振动频率的 4 倍,不是 3 倍,Do[15] 比 Do[1] 高了两个八度,相邻八度是二倍关系,所以 Do[15] 振动频率是 Do[8] 二倍,是 Do[1] 4倍。
音的历史: 纯律
大概由于人耳的听觉的关系,好听纯正的音程关系都是简单的整数倍关系。我们经常唱的 Do Re Mi Fa Sol La Ti ,是被一个个找出来的,早期音乐家们,先找到了 Do[1] , 然后确定了二倍振频关系的 Do[8] (高音 Do,因为它们听着感觉相似);
接下来,遵从整数倍关系寻找,找到 Do[1] 振动频率的 3 倍音 Sol[12] (高一个 8 度的 Sol,因为 2 倍振动频率已经是 Do[8]了),然后根据相邻一个高音间二倍振频关系,定义了 Do[1] 的 3/2 倍音程关系音为 Sol[5],3/2 倍的音程关系,也称为纯五度音程关系 。
类似的找到了 Do[1] 5 倍振频关系的音 Mi[17] (高了两个8度的 Mi),两个8度和原音之间是 4 倍振频关系,所以原音 Mi[3] 是 5/4 倍的 Do[1] 振频关系,这个振频关系在音程上被称为大三度。计算稍微有些绕,我画了张图。
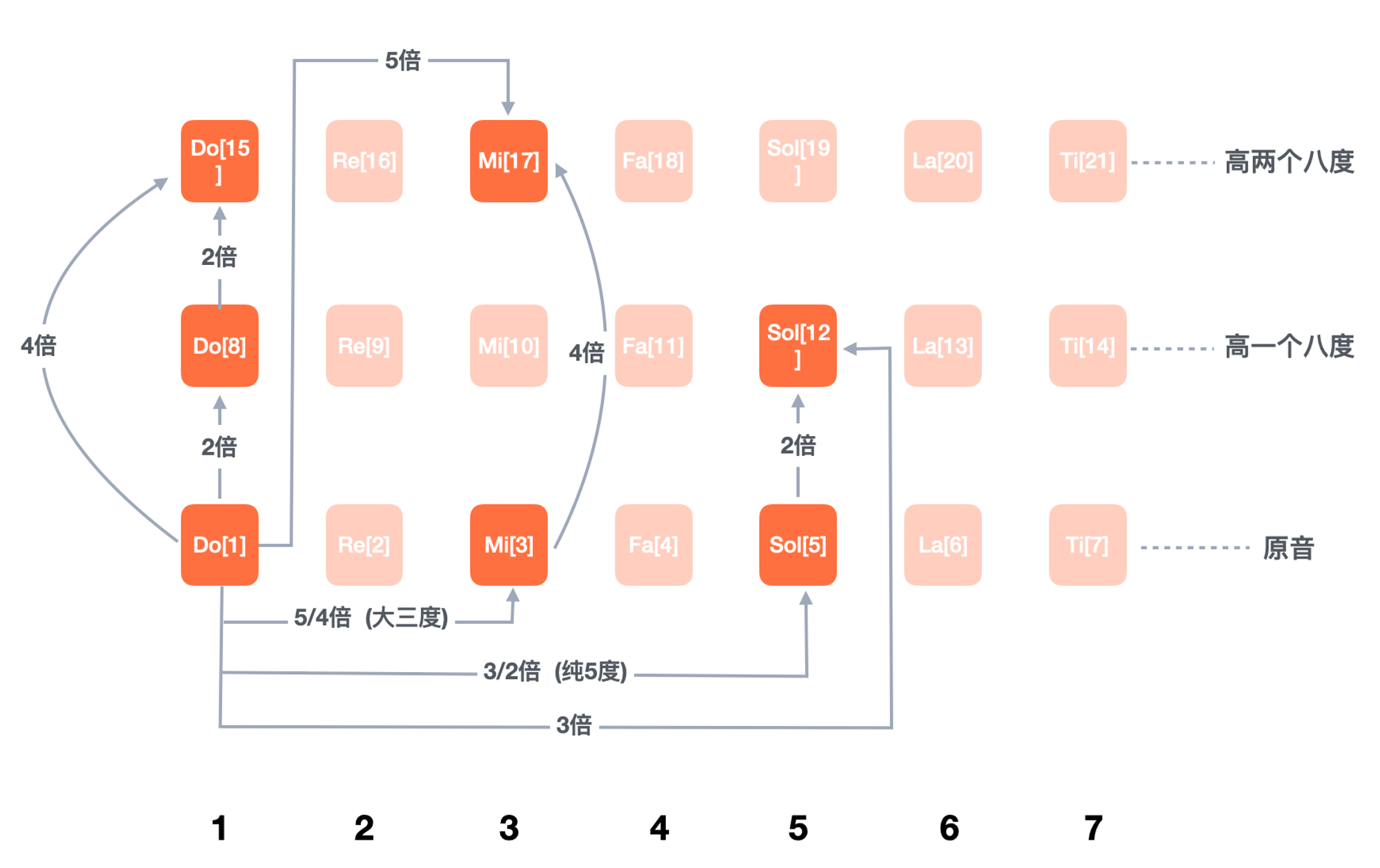
到现在,已经找到了 Do Mi Sol 三个音,然后根据 Do Mi Sol 之间的音程关系相做四则运算,找齐了 Re Fa La Ti 四个音,像这样依据大三度 (5/4 倍) 和 纯五度 (3/2 倍) 找到配出来的 Do Re Mi Fa Sol La Ti ,就被称为纯律,然而现代音乐用的并不是纯律。
纯律音程关系表
ㅤ | 唱名 | 倍数 |
1 | Do[1] | 1 |
2 | Re | 9/8 |
3 | Mi | 5/4 |
4 | Fa | 4/3 |
5 | Sol | 3/2 |
6 | La | 5/3 |
7 | Ti | 15/8 |
1* | Do[8] | 2 |
音的历史: 五度相生律
古称三分损益律,纯律是由八度(2倍)、 大三度 (5/4 倍) 和 纯五度 (3/2 倍) 衍生出来的,而五度相生律则仅由八度(2倍)、纯五度 (3/2 倍) 衍生出来。现代音乐依然不使用五度相生律。
五度相生律音程关系表
ㅤ | 唱名 | 倍数 |
1 | Do[1] | 1 |
2 | Re | 9/8 |
3 | Mi | 81/64 |
4 | Fa | 4/3 |
5 | Sol | 3/2 |
6 | La | 27/16 |
7 | Ti | 243/128 |
1* | Do[8] | 2 |
音的历史: 中国古乐曲的五声音阶
与西方音乐相比,中国的古乐曲只用到了五个音,分别是 1 2 3 5 6,少了 ‘发Fa’ 和 ‘稀Ti’ ,古乐曲给 1 2 3 5 6 起的唱名分别是 宫 商 角 徵(读zhǐ音) 羽。
ㅤ | 1 | 2 | 3 | 5 | 6 |
唱名 | 宫 | 商 | 角 | 徵 | 羽 |
成语 ‘五音不全’ 中的五音指的就是上边的五个音。现在还时有听到的江南小调《茉莉花》和岳飞词的《满江红》都是古曲,全曲若用唱名哼出,只有哆、来、咪、索、拉“,全无发、稀”两音;
当代音乐: 十二平均音律
观察纯律和五度相生律,发现音程关系太复杂,简单的口算已经无法得出,最重要的是音程关系不是平均分布(但是接近平均),这给音乐的转调带来了很大的麻烦,由于 Do Re Mi …Ti 之间音程关系不平均,想要同时升高半个音或者一个音,就不能简单的同时加上某个振频了,转调后所有音都需要重新调整,这也给乐器制造带来了困难。
所以十二平均音律诞生了,顾名思义,十二平均音律有 12 个音,并且音程关系是平均分布的。十二平均音律由 巴赫 中国明代音乐家朱载堉(yù)首次提出,并制造了世界最早的十二平均律乐器。音程关系不是根据 3、5 倍数关系得出,而是通过 2n/12 (n取值 [0…12]) 的音程关系得出,所以保证了各个音之间的音程关系是平均的,这给转调和乐器制造带来了极大的方便。
虽然十二平均音律的音程关系是基于 2n/12 得出的,但是却和纯律和五度相生律都极为接近。例如 27/12 = 1.498 ,非常接近纯律中的 $\frac{3}{2} = 1.5$ ,误差只有0.1%。
十二平均律音程关系表
ㅤ | 唱名 | 倍数 |
1 | Do[1] | 1=20/12 |
2 | Re | 22/12 |
3 | Mi | 24/12 |
4 | Fa | 25/12 |
5 | Sol | 27/12 |
6 | La | 29/12 |
7 | Ti | 211/12 |
1* | Do[8] | 2=212/12 |
观察音程表,会发现, Do - Re, Re - Mi, Fa - Sol, Sol - La, 它们之间音程关系是平均的,都相差 22/12 音程,而 Mi - Fa 和 Ti - Do[8] 之间却是 21/12 音程差距。之所以这样是因为,十二平均律中还存在着不为人们熟知的半音。
十二平均律的十二个音
既然叫十二平均律,那么就应该有十二个音;确实是这样,十二平均律有十二个音,只是我们平常见到的是 1 2 3 4 5 6 7 这 7 个音。
通过观察音程关系表,得知 Do[1] 到 Re[2] 之间音程差距是 22/12 ,而 Mi[3] 到 Fa[4] 之间音程差距是 21/12,其音程差距是 Do[1] - Re[2] 音程差距的一半。所以,Do[1] 和 Re[2] 之间还可以有个音,这个音与 Do[1] 之间的音程关系是 21/12,与 Re[2] 之间的音程关系也是 21/12,这个音读作 ?Do (升Do) 或者 ?Re (降Re)。同样 Re 和 Mi 之间也有个半音读作 ?Re 或者 ?Mi,类似的还有 Fa - Sol 、 Sol - La 和 La - Ti 之间也有个半音。
21/12 大小的音程被称为半音程,22/12 称为全音程,全音程是半音程的2倍;半音程和全音程也叫半音和全音,所以半音和全音是音程单位,好比长度单位中的厘米一样,就是个音程计量单位。 半音是最小的音程单位,全音是2倍半音,还有更大的音程计量单位叫度,比如前边提到的大三度和纯五度。还有八度也是音程单位,八度音程等同于12*半音的音程关系。
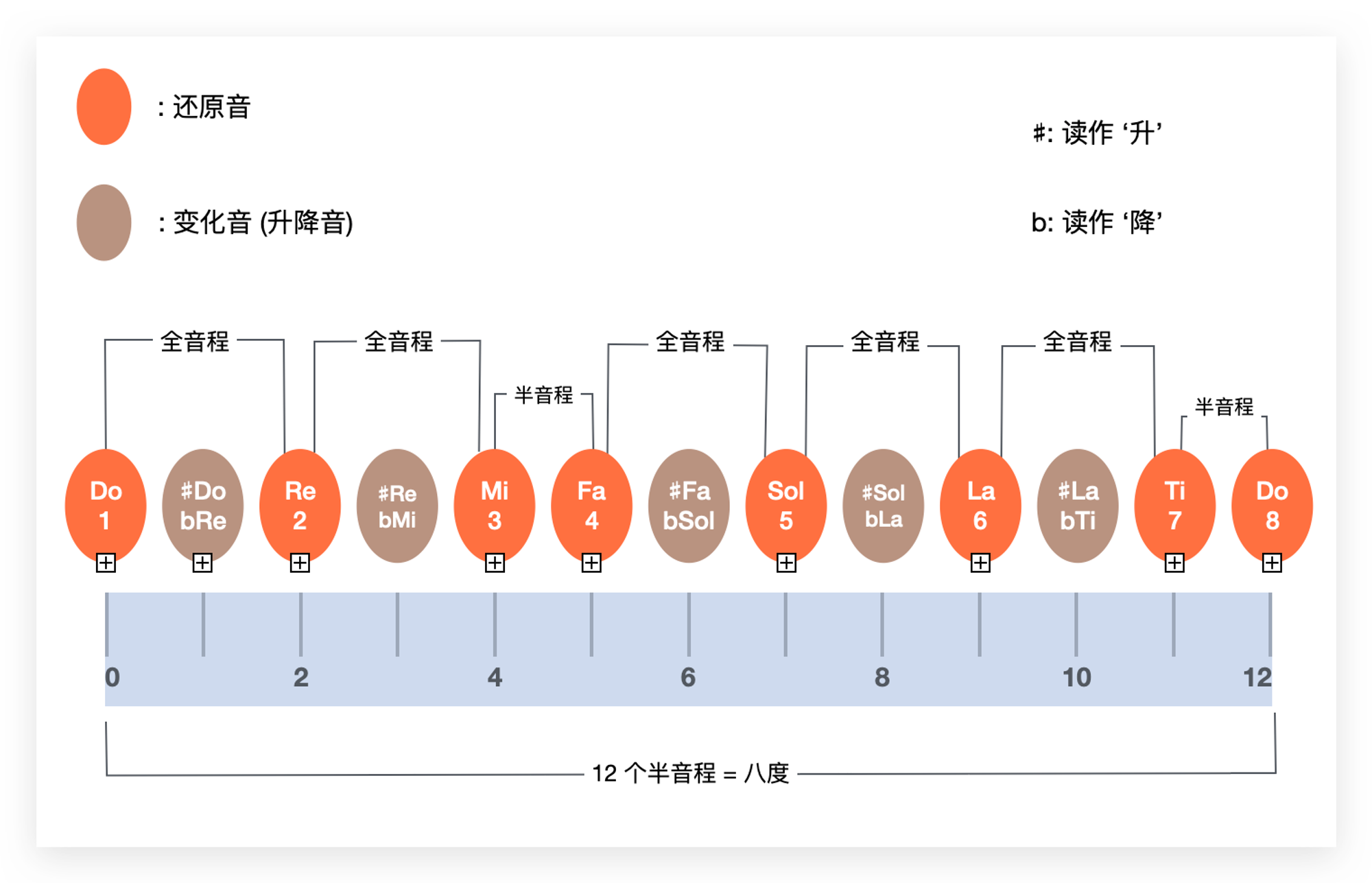
十二个音我们熟悉的 Do[1] Re[2] Mi[3] Fa[4] Sol[5] La[6] Ti[7] 称为还原音,也叫本位音或者自然音,还原音中比较特殊的是 Mi - Fa 和 Ti[7] - Do[8] 之间是半音程,其余音之间都是全音程;剩下的 5 个音,也就是读作 ‘升降’ 的5个音叫做变化音,同一个变化音可以同时用 ?(升) 或 ?(降)同时表示,例如 Do[1] 和 Re[2] 之间的音,既可以称为 #Do 也可以称为 ?Re 。每个变化音也有对应的唱名。
十二平均律中每个音对应的唱名
ㅤ | 唱名 |
1 | Do |
?1 或 ?2 | Di 或 Ra |
2 | Re |
?2 或 ?3 | Ri 或 Me |
3 | Mi |
4 | Fa |
?4 或 ?5 | Fi 或 Se |
5 | Sol |
?5 或 ?6 | Si 或 Le |
6 | La |
?6 或 ?7 | Li 或 Te |
7 | Ti |
1* | Do[8] |
可以看出,?(升) 音大部分用 i 结尾表示,比如 Di (升 Do) Ri Mi …,Ti 除外;?(降)音大部分用 e 结尾表示,例如 Me(降Mi) Se Le Te ,Re 除外,Re 的还原音就是 e 结尾。
熟悉吉他的人都知道吉他上都有一个一个小格子叫 ‘品格’ ,相邻品格之间音程关系是半个音,单独拿出一根弦,其空弦音和12品的音是同一个,只不过高了一个八度。比如吉他一弦,空弦音是 Mi (正常调弦),那么一弦 12 品就是高了一个八度的 Mi,并且 12 品是吉他弦长的中心点,可以说吉他是完全遵循了 12 平均音律的乐器。
(本文完) 非音乐专业,如有错误,欢迎指正批评。 下一篇:(乐理基础二:音程、音名、音阶、调式与音级)