很多机器学习的教程中,只管给出公式,但公式如何得来,读者并不知晓。这是我个人机器学习的第二篇博客,专门来详细的推导和解释逻辑回归,后文会有详细的数学推导过程。由于机器学习中数学符号太多,用纯文本写博客非常麻烦,索性我将自己的笔记截图贴了上来。
机器学习在解决分类问题时,理论层面依赖的是逻辑回归(logistic regression)。而要弄懂逻辑回归,首先要明白一个概率论的经典方法,最大似然估计法。最大似然估计法,是一种点估计法,通过样本来估计数学期望;求解步骤非常固定。
1、构造似然函数,即样本的概率连乘。
2、取对数(方便求导数)。
3、是否有解,有解,即为最大似然估计值。无解,则从条件的边界上找最值。
具体的后文详细介绍;这里有个问题,困扰了我很久。为什么连乘后取最大值,就是数学期望?直到前段时间,我才弄明白其中的道理。要理清楚这个问题,先要从几个基本概念说起。
样本与随机变量
几乎地球人都知道,抛掷一枚硬币,正面向上的概率为 1/2,或者 0.5,这个值还有另外一种解读,即抛 10次硬币,正面(或反面)朝上次数最有可能为 5次。但是如何证明这件事,传统的数学都能进行公式推导,但在概率论和数理统计中,显然无法通过公式推导来证明,因为,当我们讨论一个事情的概率时,侧重的是未发生的事件;就如抛硬币,默认我们讨论的是,接下来你拿出一枚硬币,抛出后正面朝上的概率。这件事显然还没有发生。
对于这件事情,我们只能通过做实验来验证。例如,接下来,我们抛10次硬币,记录每次的结果。把这10次的结果序列,称为简单随机样本,简称样本。每次可能的结果值(正面向上或反面向上)称为随机变量。为了竟可能避免偶然事件的影响,可以多来几轮实验,同时每次实验次数竟可能多一些,然后取几轮的均值,这个均值也叫样本均值。例如,一轮实验中,抛硬币100次,记录正面朝上的次数,除以总次数(100),认为是本轮实验的结果。同样的实验进行10轮。以此来估算出硬币正面向上的概率。
中心极限定理
中心极限定理表示,无论之前是什么分布,只要样本中独立同分布的随机变量足够多时,则整体分布接近于正态分布。这个定理非常重要,也是理解最大似然估计的关键所在。
还以投硬币为例,抛10次硬币,正面朝上出现的次数,可能是 1次,2次…10次。但是最有可能的应当是5次。次有可能是 4次或者 6次。接下来 3次或7次,以此类推。且只要抛的次数足够多,那么正面朝上的次数基本稳定在总次数的一半,即1/2。
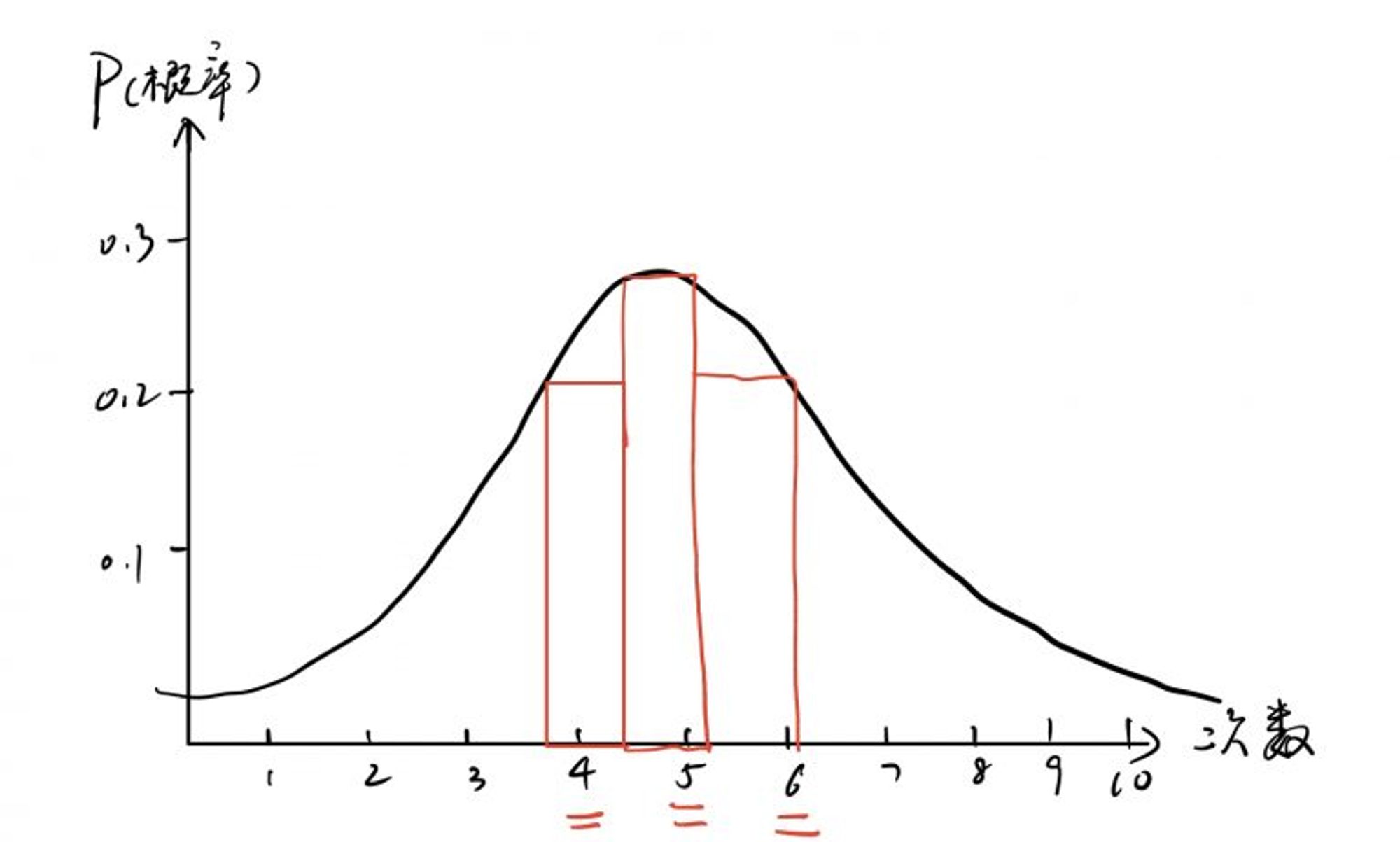
上图的函数表示,每轮进行10次抛硬币统计。多轮过后,正面朝上的次数分布图。即很多轮实验,正面朝上的次数大多集中在 4、5、6 次。这个图和正态分布的函数图形接近。
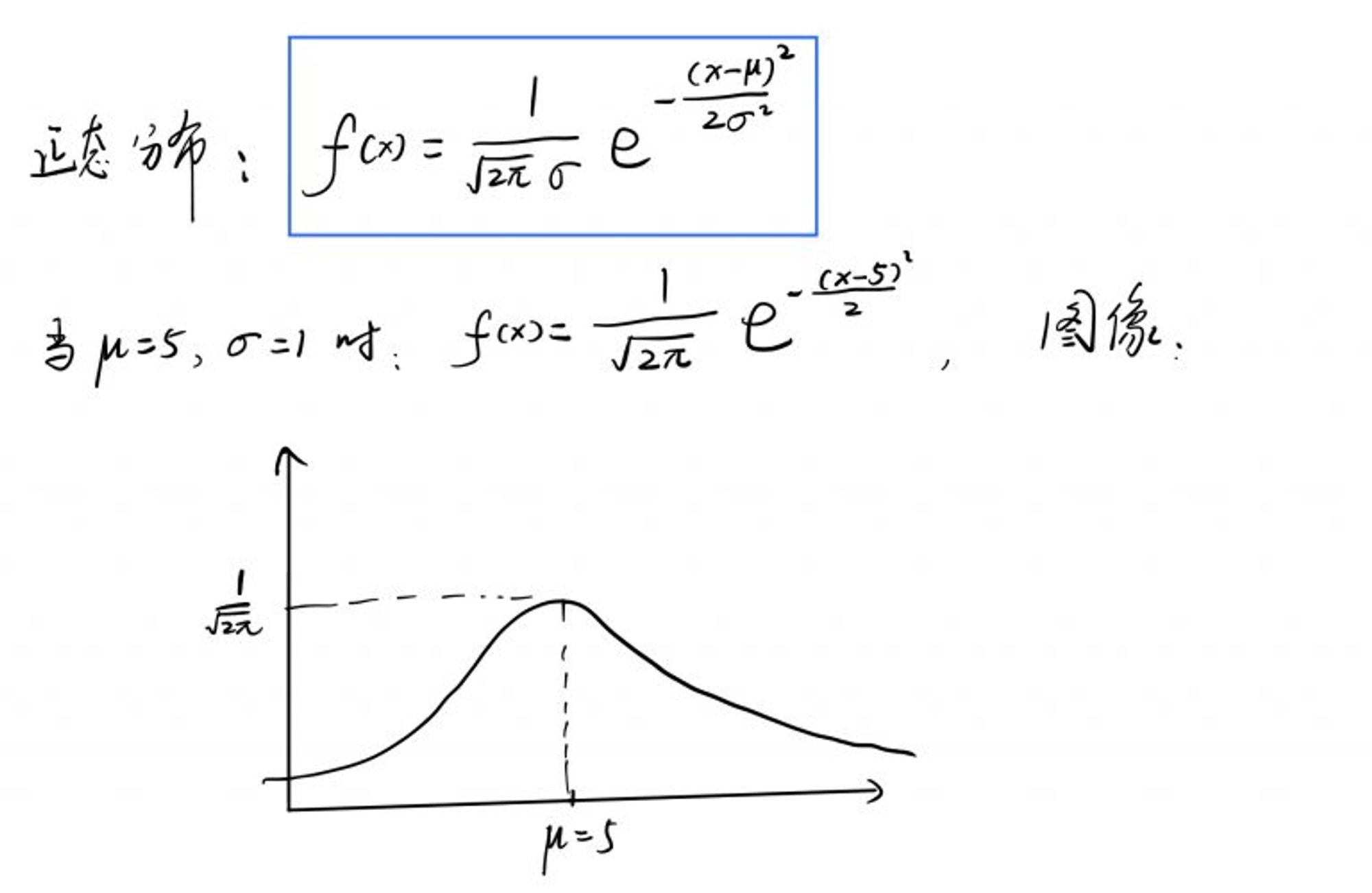
其中,μ 为数学期望,σ 为方差。
最大似然估计与参数估计
上图中,我们看到了抛10次硬币,正面朝上的次数最有可能是 x=5 次。这是因为知道了正面朝上的概率是 1/2,假设我们不知道。想通过多次样本的统计结果计算得出这个结论,这就称为参数估计,即设抛一枚硬币正面朝上的概率为 Θ,Θ 是未知参数。估计方法有很多种,这里讨论最大似然估计法。
每次抛硬币的结果只有两种,正面朝上,或者反面朝上。所以抛硬币是典型的二项分布,也叫伯努利分布,抛了 n 次硬币,即 n 重伯努利实验。设硬币正面向上的次数为 k 次,在一轮(10次)实验中,k 的取值 1…10。二项分布属于离散型分布律,概率公式如下:
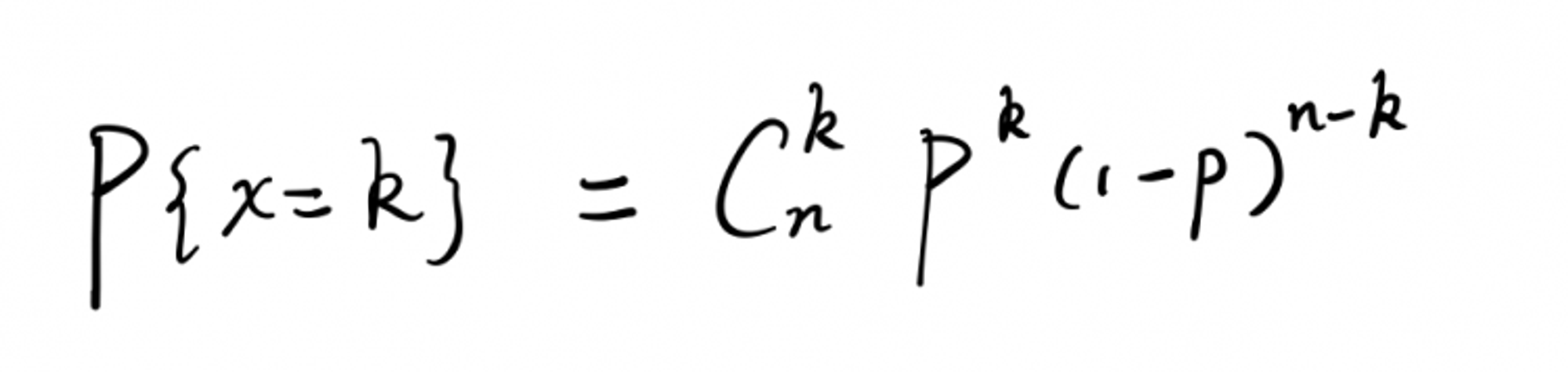
构造似然函数
前边我们介绍过,硬币正面朝上的概率 Θ 的另一种解读:抛 n 次硬币,出现正面朝上的次数为 k次,其中 k/n = Θ;又因为概率 Θ 的取值范围是
[0, 1],都是正数,所以将每个可能的概率结果连乘依然是正数。这便是构造似然函数:L(Θ) = L(X1, X2, ...Xn) = ∏ f(Xi, Θ)其中
∏是连乘符号。X1…Xn 是每轮实验的随机变量。 因为抛硬币为二项分布,所以这里的 f(Xi, Θ) 为: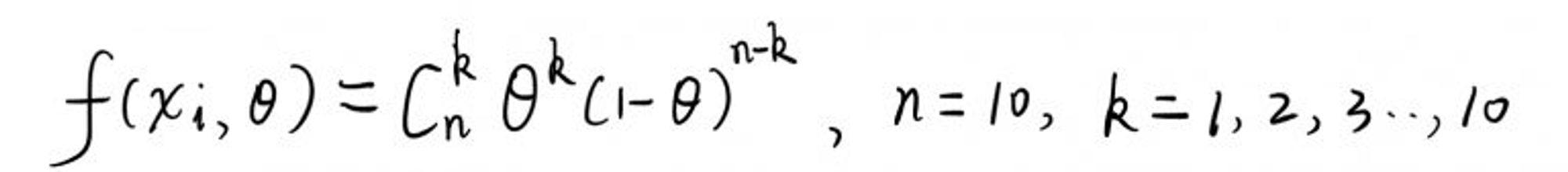
求解似然函数的最大值
已经得到似然函数,如何继续求解未知参数 Θ 呢 ? 答案是求该似然函数的最大值情况下的 Θ。这里包含了一个自解释的逻辑,根据中心极限定理,进行多组抛硬币实验,其分布律应当接近正态分布。而我们进行的多组实验的实际表现,应当遵循这个定理:
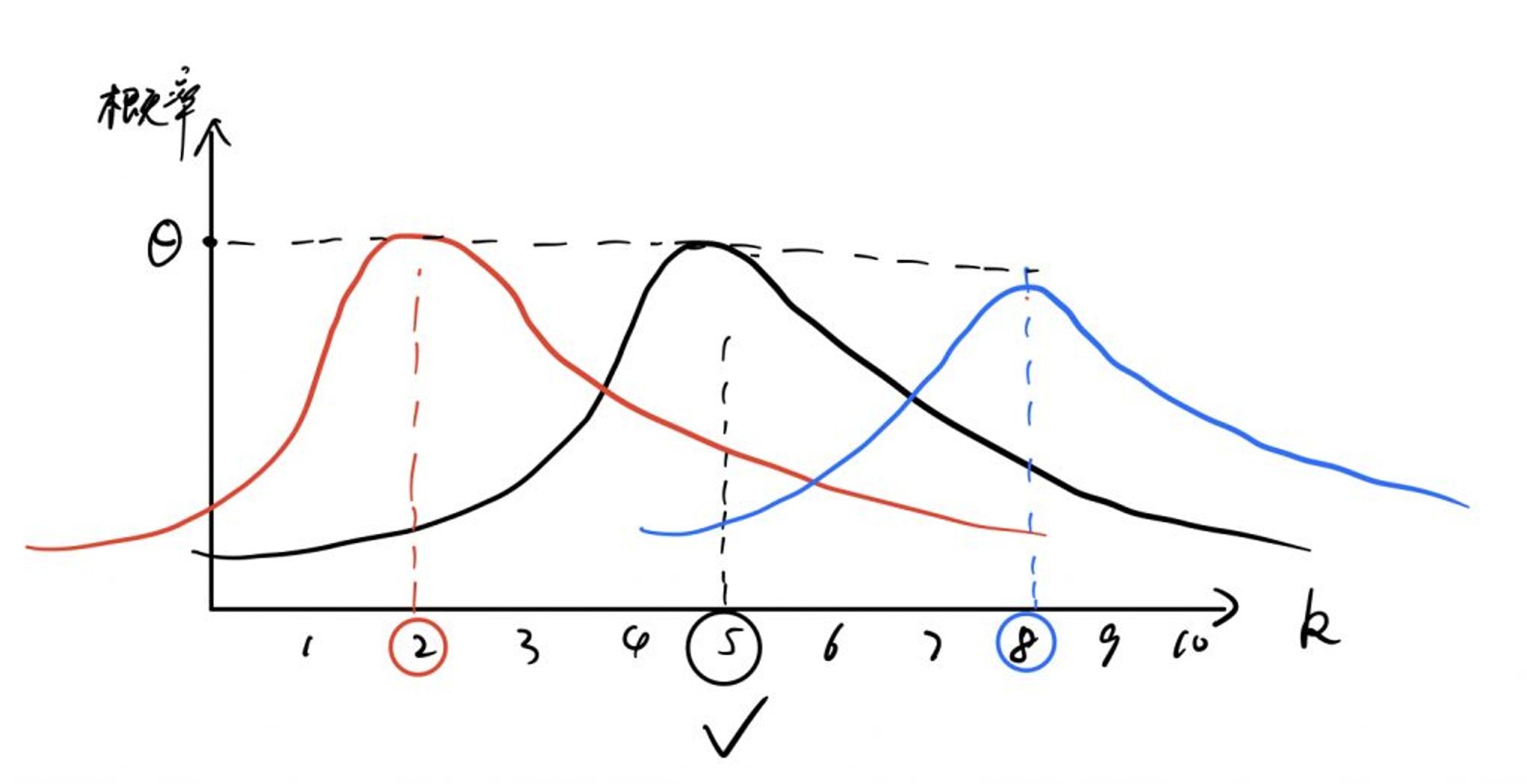
通过上帝视角,我们知道,上图中黑色的函数图像,应该是最真实的实验结果,也就是每组实验,正面朝上的次数大多应当集中在 4、5、6 这几个值。我们将每组实验结果的概率值连乘,分别带入上图中的红、黑、蓝三个函数图像,因为多次实验结果中,大部分都是 4、5、6,将概率连乘后,显然黑色函数图像的结果是最大的,而黑色函数图像正是最真实的实验结果。所以求解似然函数的最大值,然后解出未知参数 Θ 就得到了结果,因此得名最大似然估计。(这里可能不太好理解,单纯文字描述也不够详尽,读者可以多思考思考)
求最值通用的方法是求导数,而连乘函数求导数比较麻烦,可以通过先对函数取对数。由于对数函数是单调函数,所以在如果在对数函数中取得了最值点,那么该点在原函数中也是最值点。另外,对数可以将连乘函数变为和函数,从而简化运算。
取对数:
ln(L(Θ)) = ∑f(xi, Θ)接下来,求导数,求最值即可。
逻辑回归、梯度下降、损失函数
逻辑回归用于解决分类问题,而分类问题本质上就是二项分布,如果是多分类,可以看做进行多次二项分布。所以求逻辑回归的参数自然使用最大似然估计法。而在求解最值的问题上,梯度下降是一个通用方法。由于梯度下降是用来求解最小值的,所以我们让损失函数变为最小似然估计,事实上就是对最大似然估计法取相反数即可。
由于文本写数学符号很麻烦,所以下边用我的个人笔记给出详细的推导,主要推导损失函数的由来:
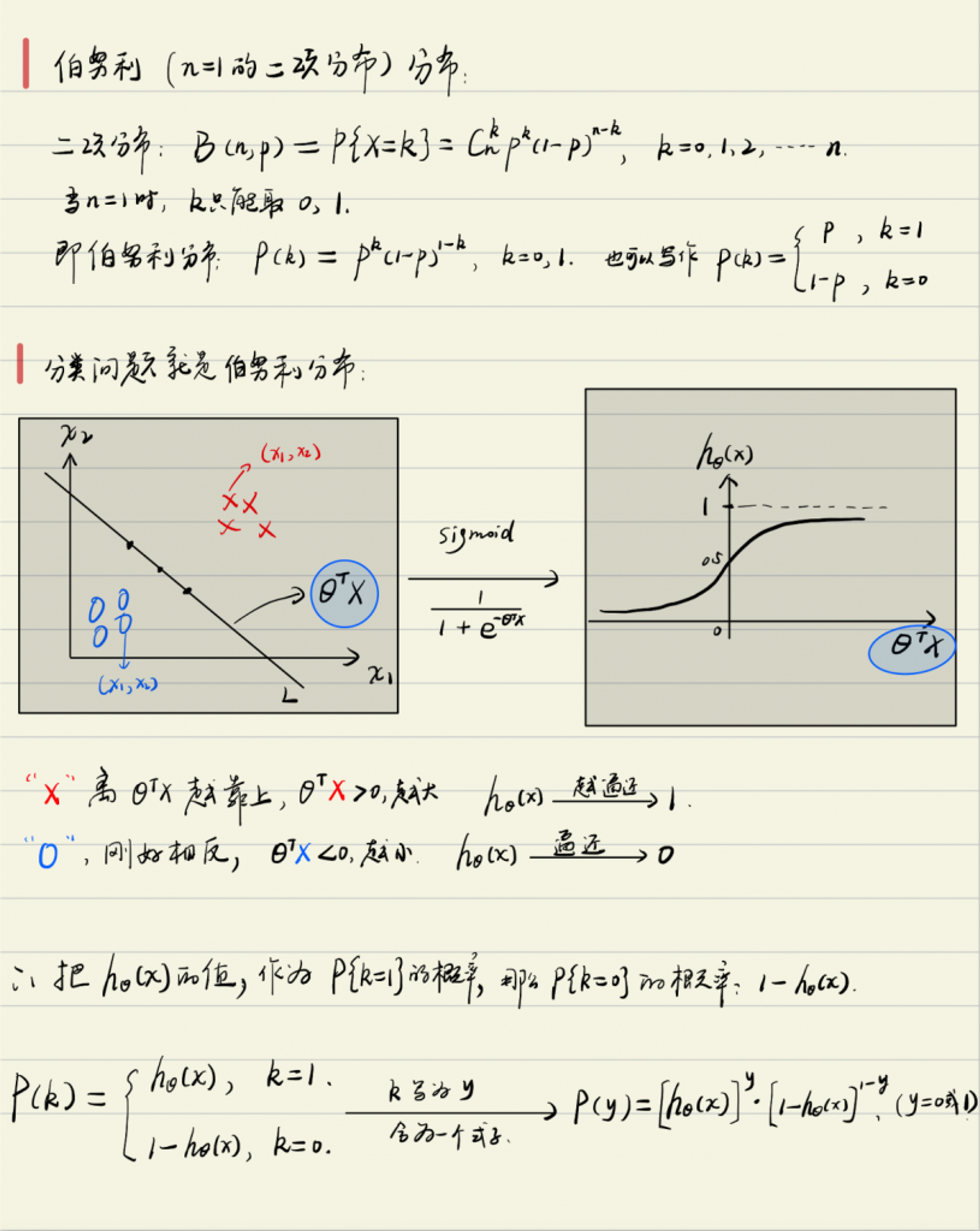

至此,便完整的推导出了损失函数。通过梯度下降,一次一次的修正损失函数的参数,最终得到最佳的参数值。即最佳的分类曲线函数。始于二项分布(0-1分布),然后通过最大似然法设计损失函数,通过梯度下降来修正参数,这个过程就叫做逻辑回归。